Lutfi Al-Sharif
Mechatronics Engineering Department,
The University of Jordan, Amman 11942, Jordan,
This email address is being protected from spambots. You need JavaScript enabled to view it.
This paper was presented at The 5th Symposium on Lift & Escalator Technology (CIBSE Lifts Group and The University of Northampton) (2014). This web version © Peters Research Ltd 2016
Keywords: elevator; lift; group control; up peak traffic; static sectoring; dynamic sectoring; destination group control; numerical methods; Monte Carlo simulation method.
Abstract
Elevator group control is critical to the optimal operation of elevator traffic systems under general traffic conditions. In the last 20 years, new elevator group control algorithms have become available for use under up-peak traffic conditions. These up-peak algorithms can be generally classified into three categories: static sectoring, dynamic sectoring and destination group control.
It is customary to use simulation to assess the effectiveness of group control algorithms. This paper offers a new approach, which is built around numerical methods.
Numerical methods can be used to objectively assess the effectiveness of an up-peak group control algorithm by subjecting the group controller to a large number of random scenarios. Each random scenario comprises a set of randomly generated passenger destinations. The performance of each scenario is recorded and the average performance of all the scenarios is used as an indicator of the effectiveness of the algorithm.
The conditions under which the scenarios are run and the algorithms executed can gradually move from the fully idealised conditions to the fully realistic conditions. There are a number of benefits to this approach which will be outlined in the paper.
1 Introduction
Elevator group control is probably the most important mathematical problem to solve in elevator systems. It is a very demanding task as it has, even for the simplest of situations, an excessively large number of possible solutions. The aim of the elevator group control algorithm is to find the solution that optimises a certain parameter of interest. The optimisation could involve one or more of the following: maximising the handling capacity, minimising the average waiting time or the average travelling time.
Elevator group control is only applicable to systems having two or more elevators operating in the same group. They have a common set of landing calls. The function of the group controller is to allocate the landing calls as soon as they are registered to one (and only one) of the elevators in the group, in order to minimise one or more of the parameters above. It is usually not possible with destination control systems to de-allocate the landing call from the elevator and re-allocate it to a different elevator in case a better allocation becomes available.
Moreover, the decision on the allocation of a new landing call to a specific elevator in the group has to be taken within a very short period of time (usually less than 500 ms). This places a large burden on the elevator group real time controller.
With the proliferation of new elevator group control algorithms, it has become necessary to objectively assess and compare these different group control algorithms. This is critical to the successful design of the vertical transportation system for a building, independently of the specific implementations that the suppliers adopt. Simulation has traditionally been the tool used to do so. This new paradigm can complement simulation in many areas.
This paper suggests a new paradigm for assessing up peak group control algorithms. It is based on two pillars: numerical scenario testing (NST) and progressive introduction of reality (PIR).
Section 2 provides an overview of the generic classifications of the elevator group control algorithms. The first pillar of the new paradigm is introduced in section 3, called the Progressive Introduction of Reality (PIR). Numerical Scenario Testing (NST) is the second pillar of the new paradigm and is introduced in section 4. Some advantages of the new paradigm are listed in section 5. Section 6 previews some results from the application of the method for a sample building. Conclusions are drawn in section 7.
2 Elevator Group Control Algorithms
Group control algorithms can be sub-divided into two main categories in accordance with the type of prevailing traffic as follows:
- General traffic group control algorithms: These group control algorithms are applied under any mix of traffic patterns (incoming; outgoing; inter-floor). Although some of the ideas presented in this paper could be applied to these group control algorithms, this will not be discussed in any detail in this paper as it is thus beyond its scope.
- Up-peak Group Control algorithms: These group control algorithms are used in cases where the main component of passenger traffic is entering the building from the main entrance and heading to the occupant floors above. This group of group control algorithms is discussed in more detail below.
It has usually been accepted that once an up-peak situation has been detected or manually selected there is very little that the group controller can do under the conventional up peak conditions other than two obvious actions. These two actions consist of returning the cars back to the main terminal as soon as they have delivered the passengers to their destinations; and controlling the status of the doors of any cars present at the main terminal in order to fill up one elevator car at a time and allow it to depart and then open the doors of other waiting cars one at a time.
However, this has changed with the introduction of a number of up-peak group control algorithms, such as static sectoring, dynamic sectoring and destination group control.
In static sectoring [1], the building is split up during the up-peak period into a number of sectors where each sector contains a number of contiguous floors having equal populations. Every time an elevator arrives at the main terminal, the elevator is assigned to a certain sector, and this is communicated to the waiting passengers at the main terminal. Dynamic sectoring operates in a similar way but with the difference that the sizes of the sectors change continuously ([2], [3], [4], [5], [6]).
Destination group control systems allow the passengers to register their destinations prior to boarding the elevator ([7], [8], [9], [10], [11]). The group control system can thus allocate the landing call to the most suitable elevator in the group and inform the passenger waiting in the lobby. As the elevator has more information, it is possible to make a better allocation decision.
The three algorithms provide an improvement in handling capacity of the elevator system. This boost attains it largest value under up peak traffic conditions ([12], [13]). The methodology outlined in this paper is suitable for assessing and comparing these three elevator group control algorithms, although the examples given have been restricted to the case of destination group control.
3 Progressive Introduction of Reality (PIR)
The first pillar that this new paradigm is based on is the concept of Progressive Introduction of Reality (PIR). The results of the assessment under fully idealized conditions are referred to as the Idealised Optimal Benchmark (IOB) which has been discussed in more detail in [12]. The IOB offers an upper limit on the performance to which all subsequent results can be compared. As real life conditions are introduced, the general rule is that the performance of the system deteriorates.
The various parameters or conditions that can be varied are shown diagrammatically in Figure 1, where fully idealized conditions are shown on the left hand-side, while real life conditions are shown on the right hand side. Of particular interest is the condition of assessing the parameters using one round trip time as the analysis workspace as opposed to using a longer period of time as the analysis workspace, where this condition is particularly important when assessing the value of the average waiting time using Monte Carlo simulation.
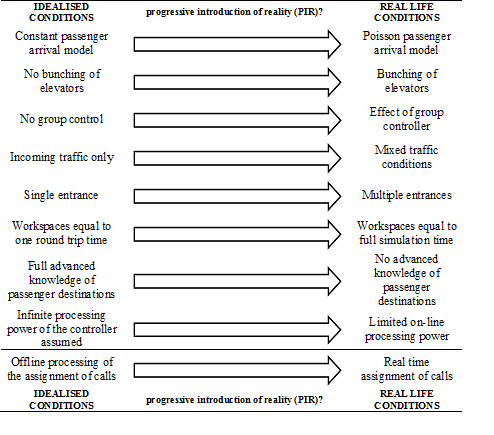
Figure 1: Diagrammatic representation of the concept of progressive introduction of reality (PIR).
The concept of PIR has also been applied in deriving a formula for the round trip time, starting from the case of single entrance, incoming traffic, equal floor heights in [14], moving to multiple entrances, incoming traffic, equal floor heights in [15], moving to multiple entrances, incoming traffic, unequal floor heights, top speed not attained in one floor journey in [16] and then ending with multiple entrance, mixed traffic condition, unequal floor heights and top speed not attained in one floor journey in [17].
4 Numerical Scenario Testing (NST)
This section outlines the methodology used for assessing the destination group control algorithm under up peak conditions ([12], [13], [18], [19]). As shown in [20] in detail, the number of possible combinations is astronomically large. It is thus not practical or realistic to list all of the possible scenarios and to enumerate every possible solution to each scenario.
A more practical solution is to take a sample of the possible scenarios using Monte Carlo simulation, and then to solve each scenario using heuristics or rules of thumb. It is also possible to solve the scenarios using other optimisation techniques (e.g. single step and multi-step random searches). These solution methods are not intended in any way to be used in real time elevator group control systems, but they are used for off-line evaluation studies.
- The following are the steps followed in assessing a group control algorithm using numerical methods:
- Generate a new possible scenario: A new scenario is generated using a random scenario generator. This is done by randomly assigning each passenger to a floor with the probabilities linked to the floor populations.
- For each of the possible scenarios generated in i above, find the most suitable solution by using heuristic (rule based) methods or by using random search techniques. The solution will show an allocation of the L·P passengers to the L elevators. The solution will attempt to optimise a certain parameter (e.g., the smallest value of the round trip time and hence the largest handling capacity).
- Steps i and ii are repeated until a large number of scenarios have been considered (e.g., 100 000 or 1 000 000).
- Once done, the average value of the best solution for all the scenarios is calculated and is used as a representative assessment of the group control algorithm.
When considering an elevator group control such as destination for example, there are a number of methods in which the L·P passengers can be allocated to the L elevators. These methods fall mainly into two broad categories: Random searches and rule based algorithms. Examples are given below:
- Fixed step size random search. Using this tool, the software randomly makes a single change in the allocation by swapping the allocation of two passengers to two different elevators. If the optimisation target is reduced, then the swap is retained; otherwise it is rejected. This process is repeated until no more improvement can be achieved after a certain number of steps.
- Rule based allocation. Using this tool, a set of rules guides the user to splitting the sectors in the building such that the target parameter is optimised.
5 Advantages of the Paradigm
Using this paradigm for assessing the effectiveness of up-peak group control algorithms offers the following advantages, among many others:
- The effect of each introduction of a reality condition can be assessed independently of the other changes. This can be insightful to the designer of the algorithm in understanding the impact of each condition, and can be helpful in guiding the designer of the algorithm to make useful changes.
- The numerical scenario testing is transparent and can be easily described by the use of rules and heuristics, allowing reproducibility.
- It provides an overall limit on the performance of the algorithms, and thus the designer need not spend too much time on trying to improve an algorithm that is very near the benchmark.
6 Sample Results
A sample of the results found so far will be given in this section for destination group control. In assessing the destination group control algorithm operating under peak traffic conditions, four distinct stages can be traversed in moving from idealised conditions to real life conditions, as shown in Figure 2 below. The first stage is to develop an idealised optimal benchmark using equations. The next stage is generating random scenarios and solving them offline, assuming perfect advanced knowledge of the passenger destination. This is referred to as offline allocation of landing calls. The next stage is real time allocation of the landing calls, where only one landing call is revealed to the controller at a time. The final stage is real time simulation of the whole system, which then takes into consideration the movement of the elevator cars. The boost in handling capacity progressively deteriorates with the transition at every stage.
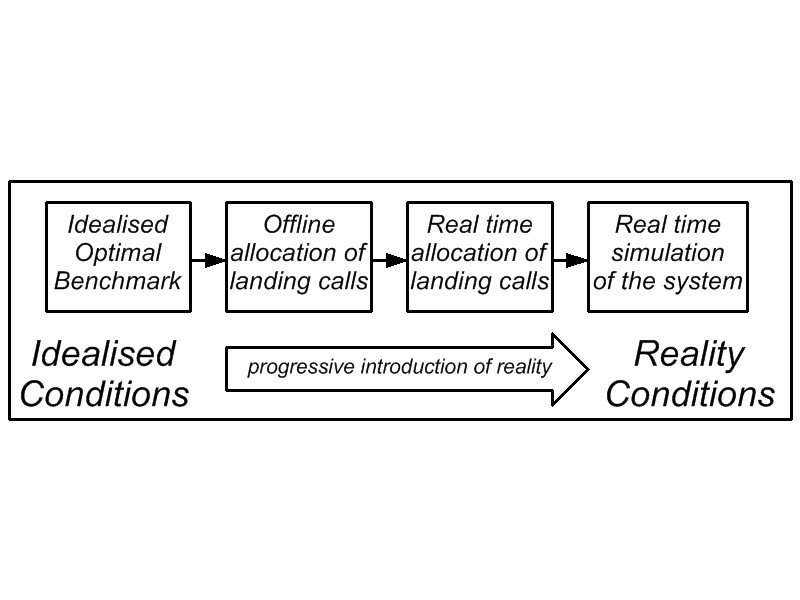
Figure 2: Applying the concept of PIR to the analysis of the performance of destination group control algorithms.
This has been applied to a single entrance sample building that has the parameters shown in Table 1 below.
Table 1: Sample building used.
| Number of Elevators in the group (L) | 4 |
| Number of Passengers in the Car (P) | 7 |
| Number of floors above the main entrance (N) | 10 |
| Total building population (U) | 600 |
| Floor height in m (df) | 4.2 |
The boost in handling capacity compared to the conventional group control has been used as the benchmark for comparison of the effectiveness of each reality condition. The boost in handling capacity has been shown for the benchmark, offline allocation and real-time allocation of calls in Table 2, where the boost in handling capacity with the IOB is 148% (i.e., an increase of 48%). Full details of the workings of the real time allocation and the effect of the number of elevators in the group can be found in [21].
Table 2: Sample results for a building under destination group control that aims to minimise the average round trip time or maximise the handling capacity of the system assuming contiguous equal size sectors.
| Algorithm/Equation | Boost in Handling Capacity |
| Idealised Optimal Benchmark (IOB) [12] | 148% |
| Minimisation of H then S (offline allocation) [13] | 142% |
| Minimisation of H only (offline allocation) [13] | 140% |
| Minimisation of S only (offline allocation) [13] | 134% |
| Real time allocation [21] | 125% |
7 Conclusions
Elevator group control algorithms can be generally sub-divided into general traffic condition algorithms and up-peak traffic condition algorithms. The up-peak group control algorithms can be further sub-divided into three types: static sectoring, dynamic sectoring and destination group control algorithms.
Simulation has traditionally been used as the tool for assessing the effectiveness of elevator group control algorithms. This paper presents a suggested new paradigm that relies on the use of numerical scenario testing (NST) and progressive introduction of reality (PIR) in order to assess the effectiveness of up peak group control algorithms. Under numerical scenario testing, the Monte Carlo simulation method is used whereby random passenger destinations are generated and the optimum solution is found for each scenario and recorded. The average of all the large number of trials is then calculated and used as representative of the performance of the algorithm, under the conditions assumed. The progressive introduction of reality starts the analysis under the most ideal conditions and then progressively changes the conditions to more real life conditions.
The advantages of this new paradigm is that it is fully transparent thus allowing reproducibility, provides insights to the algorithm designer regarding the effect of different conditions on the effectiveness of the algorithm and provides an upper limit benchmark that no algorithm can ever surpass.
Results were presented for a sample building in which the method was applied for the assessment of an algorithm for destination group control. The resultant boost in handling capacity was 148% under the idealised conditions and dropped to 125% for the real time allocation of landing calls conditions.
REFERENCES
- Bruce Powell, “Important issues in up peak traffic handling”, in Elevator Technology 4, International Association of Elevator Engineers, Proceedings of Elevcon ’92, May 1992, Amsterdam, The Netherlands, pp 207-218.
- W. L. Chan and Albert T. P. So, “Dynamic zoning for intelligent supervisory control”, International Journal of Elevator Engineering, Volume 1, 1996, pp 47-59.
- W. L. Chan and Albert T. P. So, “Dynamic zoning in elevator traffic control”, in Elevator Technology 6, International Association of Elevator Engineers, Proceedings of Elevcon ’95, March 1995, Hong Kong, pp 133-140.
- Zhonghua Li, Zongyuan Mao and Jianping Wu, “Research on Dynamic Zoning of Elevator Traffic Based on Artificial Immune Algorithm”, 8th International Conference on Control, Automation, Robotics and Vision”, Kumming, China, 6th-9th December 2004.
- Albert T.P. So, J.K.L. Yu, “Intelligent supervisory control for lifts: dynamic zoning”, Building Services Engineering Research & Technology, Volume 22, Issue 1, 2001, pp. 14-33.
- Suying Yang, Jianzhe Tai, Cheng Shao, “Dynamic partition of elevator group control system with destination floor guidance in up-peak traffic”, Journal of Computers, Volume 4, Number 1, January 2009, pp 45-52.
- Richard Peters, “Understanding the benefits and limitations of destination dispatch”, in Elevator Technology 16, The International Association of Elevator Engineers, the proceedings of Elevcon 2006, June 2006, Helsinki, Finland, pp 258-269.
- Rory Smith, Richard Peters, “ETD algorithm with destination dispatch and booster options”, in Elevator Technology 12, International Association of Elevator Engineers, Proceedings of Elevcon 2002, Milan, Italy, 2002, pp 247-257.
- Schroeder, J., “Elevatoring calculation, probable stops and reversal floor, “M10” destination halls calls + instant call assignments”, in Elevator Technology 3, Proceedings of Elevcon ’90, International Association of Elevator Engineers, 1990, pp 199-204.
- Janne Sorsa, Henri Hakonen, Marja-Liisa Siikonen, “Elevator selection with destination control system”, in Elevator Technology 15, International Association of Elevator Engineers, Proceedings of Elevcon 2005, Peking, China.
- Jorg Lauener, “Traffic performance of elevators with destination control”, Elevator World, September 2007, pp 86-94.
- Al-Sharif L, Hamdan J, Hussein M, et al. Establishing the upper performance limit of destination elevator group control using idealised optimal benchmarks (IOB). Build Service Eng Res Technol (submitted March 2014) (under review).
- Al-Sharif L, Hamdan J, Jaber Z, et al. The effect of the number of elevators in a group on the upper performance limit of destination group control. Am J Math Manage Sci (submitted February 2014) (under review).
- G.C. Barney, “Elevator Traffic Handbook: Theory and Practice”, Taylor & Francis, 2002.
- Lutfi Al-Sharif, “The effect of multiple entrances on the elevator round trip time under up-peak traffic”, Mathematical and Computer Modelling 52(3-4):545-555 (2010).
- Lutfi Al-Sharif, Ahmad M. Abu Alqumsan, Rasha Khaleel, “Derivation of a Universal Elevator Round Trip Time Formula under Incoming Traffic with Stepwise Verification”, Building Services Engineering Research and Technology, 2014, Vol. 35 issue 2, pp 198–213, doi 0143624413481685.
- Lutfi Al-Sharif and Ahmad M Abu Alqumsan, “Stepwise derivation and verification of a universal elevator round trip time formula for general traffic conditions”, Building Services Engineering Research & Technology, published online before print, DOI: 10.1177/0143624414542111.
- Moh’d M. Malak, Daoud Tuffaha, Mohamed Hussein, “Modeling and Simulation of dynamic sectoring in Elevator Traffic Analysis and Control”, final year graduation project, Supervisor: Dr. Lutfi Al-Sharif, Mechatronics Engineering Department, The University of Jordan, December 2012.
- Khaled Alkiswani, Haneen Almahmoud, “Elevator Group Control System Simulation based on Destination Group Control”, final year graduation project, Supervisor: Dr. Lutfi Al-Sharif, Mechatronics Engineering Department, The University of Jordan, May 2013.
- Lutfi Al-Sharif, Mohamed Hussein, Moh’d Malak, Daoud Tuffaha, “The Use of Numerical Methods to Evaluate the Performance of Up Peak Group Control Algorithms”, Proceedings of Elevcon 2014, Paris, 8th to 10th July 2014, pp 327-337.
- Lutfi Al-Sharif, Anas Riyal, Zaid Jaber, Jamal Hamdan, “Assessing the Up-Peak Performance of Destination Elevator Group Control Systems using Real Time Allocation of Landing Calls”, The Scientific World Journal, (submitted May 2014), (under review).
BIOGRAPHICAL DETAILS
Lutfi Al-Sharif received his Ph.D. in lift traffic analysis in 1992 from the University of Manchester. He worked for 9 years for London Underground, London, United Kingdom in the area of lifts and escalators. In 2002, he formed Al-Sharif VTC Ltd, a vertical transportation consultancy based in London, United Kingdom. He has 17 published papers in peer reviewed journals the area of vertical transportation systems and is co-inventor of four patents. He is currently Associate Professor in the Department of Mechatronic Engineering at The University of Jordan, Amman, Jordan.
